This page gives an expanded explanation of the parameters in the sensor_msgs/CameraInfo message. Please also see the comments in the message header file of CameraInfo, and the calibration wiki pages.
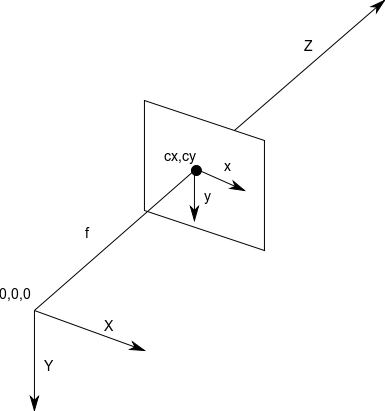
Camera coordinate system
Below is a diagram of the camera coordinate system assumed by the CameraInfo message. It is a right-handed system, with the world X and Y aligned with the image x and y. This is the same coordinate system used in OpenCV. It differs from the coordinate system of Harley and Zisserman, which has Z forward, Y up, and X to the left (looking towards +Z).
Derivation diagram
Below is a diagram of the various images that are conceptually derivable from the CameraInfo message. The boxed variables are present in this message.
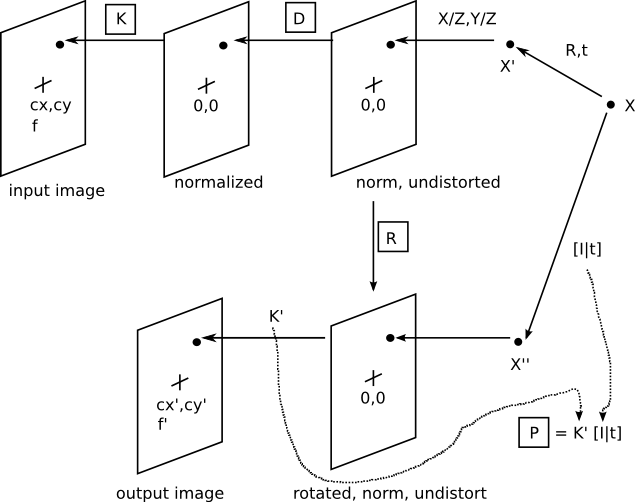
Projection onto the original image
Starting with an initial 3D point X, the position of the corresponding image point is found by going right-to-left in the upper half of the diagram. The process is summarized by the following equations.
X' = [R,t]X transform sx = X' projection x* = d(x) distortion q = Kx* pixel coordinates
This process uses the K camera matrix and D distortion vector from CameraInfo. Ignoring the transform T, you can find the projection of a point X' into the original camera frame using these equations. First, the 3D point X' is projected onto the normalized, undistorted image via a projection operation (division by Z). Then the distortion coefficients are used in the function d() to move the point to its distorted position, still in a normalized image. Finally, the normalized image is converted to a pixel-coordinate image by applying the camera matrix to each image point.
Rectification
Rectification is the process of transforming the input image into an output image with the distortion corrected, and optionally the normalized image plane transformed by rotation, optinain-image-plane translation, and optionally in-image-plane scale.
Simple monocular rectification
In this case, there is a monocular device with distortion correction only. To transform a pixel in the input image into one in the output image, it is sent through the K - D - R - K' series of transformations. K - D gets to the normalized, undistorted image; the rotation R is the identity because we don't want to rotate the normalized undistorted image; and then K' converts back to pixel coordinates in the output image. In this case, since there is no need of in-image-plane translation, or scaling from the original image, so K = K' , and only the K and D elements of CameraInfo are needed. But since ROS Electric, the camera_calibration package does monocular calibration to get K' using OpenCV's getOptimalNewCameraMatrix() function with argument 'alpha'=0.0 that cause K' ≠ K.
Projection onto the output image is by the P matrix, which is formed from K' and the optional rotation and translation, in this case the identity and 0, respectively. So if K' = K, P is redundant information, and could be formed directly from K.
Stereo and complex monocular rectification
After getting normalized undistorted image using K and D, here we apply a transformation to the normalized, undistorted image: each points on this image is rotated by R and then is passed to K' get the correspondent pixel coordinate on the output image which is translated and scaled by K'with respect to the original image. This transformation is important, for example, in aligning two images of a stereo pair to lie in the same plane and have coincident epipolar lines.
The transform of a pixel from the input to output image is the same as in the simple monocular case, except that R need not be the identity, and K' need not be equal to K. As a consequence, the normalized undistorted image can be rotated in 3D space, and the output image can be translated, scaled relative to the original image.
The projection matrix has an additional parameter, a translational offset t. This parameter is used in the right stereo camera to reflect its external position relative to the left camera. Since the point X in left camera frame is transformed to the right camera by [I|t], that means the position of the left camera frame origin with respect to the right camera frame is given by the vector t in the right camera frame.
Putting this all together, the projection matrix for the rectified output image is given by:
P = K' [I|t].
Note that in this case the internal camera parameters of the output image, K' , can be different from the input image, so P cannot be formed just from K and D. And the I is the 3x3 rotation matrix representing left camera frame in the right, not the identity.







