Contents
Author(s): Jacobo Torres (of We-R22), Mariana Sosa (of We-R22), Edgar Alfredo Portilla, José Alejandro Vásquez, Luis Felipe Marín.
Maintainer(s): Mariana Sosa, Jacobo Torres, José Alejandro Vásquez, Edgar Alfredo Portilla, Luis Felipe Marín.
License: BSD-3
Website: http://wiki.ros.org/pid_tuning
Source: https://github.com/We-R22/pid_tuning.git
API documentation:
Summary
With this ROS package you can automatically tune your PID ROS-based controllers simultaneously for both, one joint at a time or all the joints of your robot at the same time, in an easy way. This ROS package tackles the problem of pid tuning using as approach a Constrained Numerical Optimization Problem (CNOP) solved by bio-inspired algorithms, that are the baselines of this package (ready to use). You only need a set of joint trajectories and optionally Cartesian space trajectories of the robot for a specific task.
NOTE: This package is intended to be used for Gazebo simulations and has not been adapted for real robots at the moment.
Package description
The central objective for solving the CNOP is to find the ideal PID gains in order to minimize both the joint error (the difference between the desired joint trajectory and the current position of each joint) and the floating base position error (the difference between the desired Cartesian trajectory and the current Cartesian position of the link we want to track). In Figure 1 you can see how the joint trajectory and the floating base trajectory are represented for each compatible robot morphology with the package:
a. Legged Robots
b. Differential Robots (Wheeled Robots)
c. Robot Manipulators
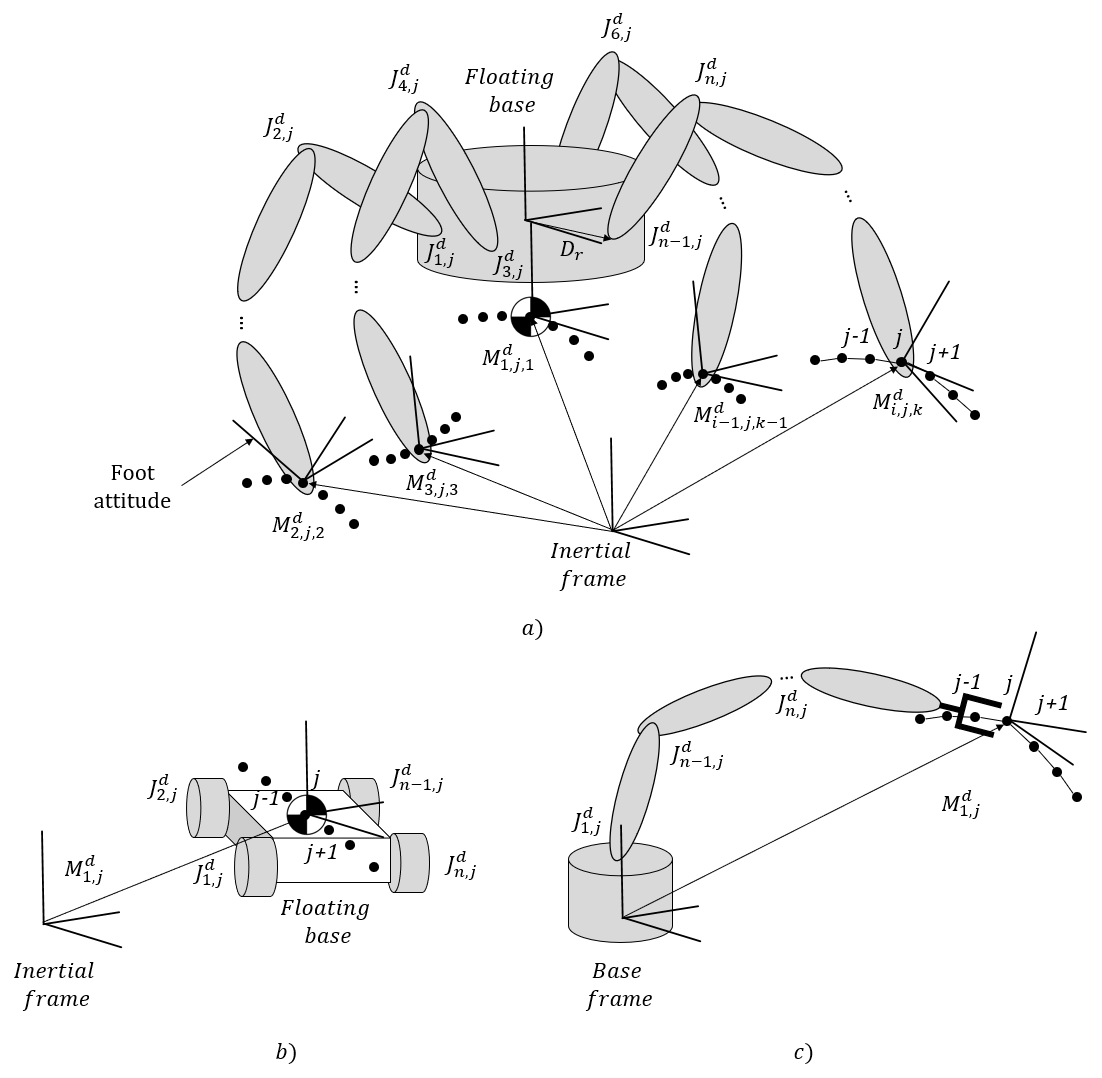
Where J and M are the discrete trajectories of the joint and cartesian space respectively needed for the implementation.
For this purpose, the package pid_tuning implements an automatic mechanism for tuning the PID gains of the ros_controllers by using bio-inspired algorithms with Gazebo. The architecture is structured as shown in Figure 2.
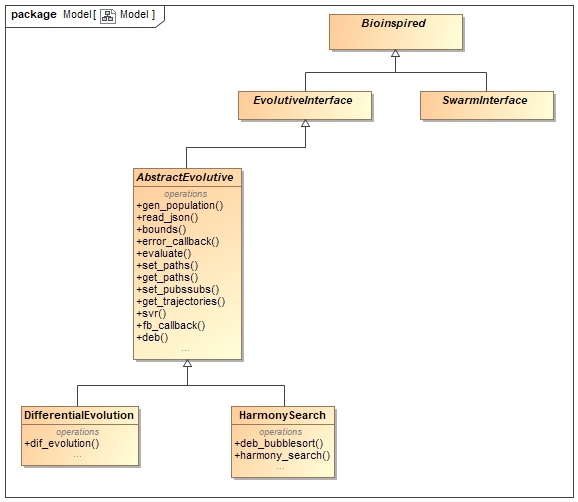
As you can see in the previous figure, you can choose between using evolutive algorithms or swarm algorithms. At the moment we only have implemented two evolutive algorithms: Differential Evolution (DE in its version DE/rand/1/bin) and Harmony Search. Evolutive Algorithms have similar operations, their process is shown in Figure 1.
After selecting between one of the Evolutive Algorithms, you need to choose between two options depending on the level of accuracy that you want or need, these options are:
Sending the joint and floating base trajectories: this will consider both the joint error and the floating base error, this means it will not only take in count the accuracy in joint space but in the trajectory following task too (Cartesian space). In optimization this is approached as a Constrained Numerical Optimization Problem (CNOP).
Sending the joint trajectories: this will only consider the joint error, In optimization this is known as Unconstrained Numerical Optimization Problem, which is a particular case of a CNOP.
Population
As you can see in the Figure 1, the process starts with the generation of a random population, which is a Nxm matrix, in this specific case of PID tuning, the matrix has as many rows as individuals (N) and m=3A+2 elements for columns, where A is the number of joints and 3A are the PID gains, Kp, Ki and Kd, considering all the controlled joints. The second term (+2) in the m equation, are the Objective Function (OF) and the Sum of Constraint Violation (SCV) columns. Where the Objective Function is the sum of all joint errors (joint space) and the SCV is calculated considering an Equality Constraint defined as the sum of position error measured at the floating base link along the Cartesian trajectory, based on a Constraint Handler in this case, Deb's feasibility rules. If you want to implement the constraint approach you will need to get the current position of the floating base link, thus you need to build an odometry node that publishes the odometry data in the topic: /odom , the pid_tuning algorithms will automatically subscribe to this topic, so you don’t need to modify anything inside the pid_tuning classes.
Then, each individual of the first generation gets evaluated in Gazebo, one after the other, restarting both the Gazebo simulation and controllers once an individual has finished the evaluation, this is done by updating the PID gains in the rosparam and sending the joint trajectories to the /pid/command topic, and calculating the OF using the data error available in the /pid/state topic and SCV is calculated using the odometry data.
In order to achieve this without trouble in Gazebo, a class has been created to control the flow simulation, for example: stop, restart, pause, unpause and reset the controllers in the Gazebo environment. This class is just used internally by the algorithms and you do not need to modify it.
After the evaluation of the first generation, the evaluated population has to be sent to one of the evolutive algorithms, at the moment we have Differential Evolution and Harmony Search which will be described below.
Differential Evolution
DE is based on "Differential Mutation" which in its rand/1/bin version consists of adding to a vector of the population, the scaled difference between two vectors taken from the same population, in order to direct the search considering two operands: mutant factor F and crossing factor C. Although originally DE was designed for unconstrained optimization problems, it is possible to incorporate a constraint handler for solving CNOP cases. Thus, two operators are required:
F = floating number between 0 and 1
C = floating number between 0 and 1
This parameters must be specified by the user in the implementation
Applying this mechanism, the algorithm creates a "children population matrix" which is evaluated and then compared to their parents; only the best individuals between the two matrices will pass to the next generation.
After iterating a certain number of generation or completing one of the stopping criteria, the algorithm will return the best individual of all generations, which will represent the ideal PID gains for the controllers of the robot.
Harmony Search
Harmony Search is mainly inspired in musical improvisation, on how musicians compose and find new harmonies; they do this based on their experience and improvising new harmonies combining what they've already learn and new ideas. In this case, the population matrix is called Harmony Memory and each individual is named a harmony composed by m-2 notes.
The Harmony Search algorithm requires 3 operators:
r_accept = r acceptance (random number between 0 and 1)
r_pa = pitch adjustment (value between 0 and 1)
bw = band width (value close to 0, if 0, the algorithm will automatically calculate bw by applying an equation)
Requirements
You need to install numpy and pandas.
Installation
Here you'll find a description on how you can install the pid_tuning package in your workspace so you can use it for your projects.
- In the terminal, move to the catkin workspace in which you have your robot description package.
cd ~/<workspace_name>/src
- Clone the github package repository
git clone https://github.com/We-R22/pid_tuning.git
- Return to your workspace
cd ~/<workspace_name>
- Compile the workspace
catkin_make
- Add to the bash
source devel/setup.bash
Tutorials
We created a set of step by step Tutorials, you can get started on the Impementation of pid_tuning in a SCARA robot. We will add more tutorials ASAP.







