Only released in EOL distros:
Package Summary
A node to control nonlinear dynamic systems
- Maintainer status: developed
- Maintainer: Andy Zelenak <andyz AT utexas DOT edu>
- Author: Andy Zelenak <andyz AT utexas DOT edu>
- License: BSD
- Source: git https://bitbucket.org/AndyZe/lyap_control.git (branch: master)
Package Summary
A node to control nonlinear dynamic systems
- Maintainer status: maintained
- Maintainer: Andy Zelenak <andyz AT utexas DOT edu>
- Author: Andy Zelenak <andyz AT utexas DOT edu>
- License: BSD
- Source: git https://bitbucket.org/AndyZe/lyap_control.git (branch: master)
Package Summary
A node to control nonlinear dynamic systems
- Maintainer status: maintained
- Maintainer: Andy Zelenak <andyz AT utexas DOT edu>
- Author: Andy Zelenak <andyz AT utexas DOT edu>
- License: BSD
- Source: git https://bitbucket.org/AndyZe/lyap_control.git (branch: master)
Contents
The lyap_control package provides a sophisticated and relatively easy-to-use control node. It can handle regulation or tracking problems of any order and with any number of inputs... from simple first order dynamic systems where a PID controller would typically be used... up to complex, large, higher-order systems. There is also a MATLAB simulator which can be used to visualize, tune, and simulate the control algorithm beforehand. The default example of the MATLAB toolbox shows the simultaneous tracking of seven motors. The theory behind the algorithm is explained here.
Installing the package
At this point, it's best to install this package from source. Create a catkin workspace for the package:
$ mkdir -p ~/Desktop/catkin_ws/src $ cd ~/Desktop/catkin_ws/src $ catkin_init_workspace
Clone the package
$ git clone https://bitbucket.org/AndyZe/lyap_control.git $ cd ..
Build the package
$ catkin_make
Source the new files
$ source devel/setup.bash
(You may have to do this every time you open a new terminal window, or add this line to your bashrc: source ~/Desktop/catkin_ws/devel/setup.bash)
Check that it runs
$ roslaunch lyap_control lyap_control.launch
This launches a simulation of a 2nd-order system with (1,-2) setpoints. The displayed V is the sum-of-squares of the error for all states (it should drop exponentially).
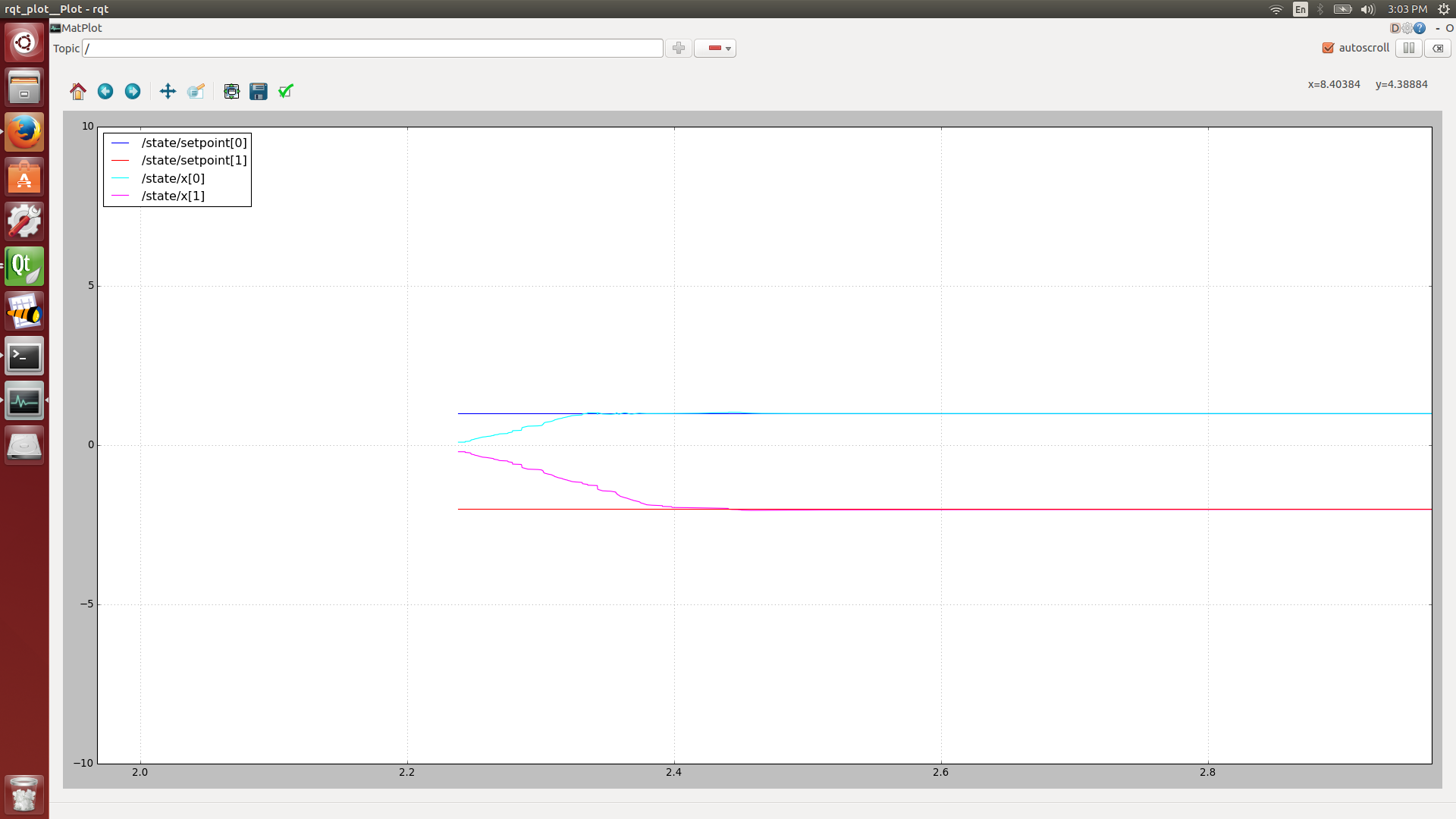
Running the default 2nd-order example
To run the controller nodes individually:
$ roscore $ rosrun lyap_control controller (publishes data on the control_effort topic) $ rosrun lyap_control second_order_plant (publishes data on the state topic)
You may wish to tune the controller at this point. You can adjust its 'aggressiveness', called V_dot_target_initial_dB, in controller.h. Generally a more negative value performs better, unless the time step is too small and it becomes unstable. The saturation limits on the control effort (maximum and minimum) and the controller's model of the system are also adjusted here.
The time step for the simulation is adjusted as the variable delta_t in second_order_plant_header.h. A smaller time step will perform better.
Running a first-order system
To demonstrate how to switch to a different dynamic system, a first-order single-input example is included (first_order_plant_sim.cpp). Here are the changes that must be made to control this other system:
1. In controller.h, change high_saturation_limit and low_saturation_limit to one-vectors since there is one input now.
2. Edit the model definition in controller.h to update the controller's model of the system. Comment the second equation so there is just one state variable
3. Since there are fewer states and inputs, the messages that the nodes pass must be shorter. In controller.msg, update u to a 1-vector. In plant.msg, update x and setpoint to 1-vectors.
That's it! Now run the system again--
$ catkin_make
$ roscore
$ rosrun lyap_control controller
$ rosrun lyap_control first_order_plant
and you should see the system stabilize at 1.0.
If you wish to change the initial conditions or the setpoints, or even make a time-varying setpoint, you can do so in first_order_plant.cpp. If you want more aggressive gain, again, change V_dot_target_initial_dB in controller.h.
Recommendations for best performance
In general, the best results are achieved with a very high control rate and a very large 'gain.' Set the loop rate of your plant and the controller as fast as the hardware will allow, then set the gain (a.k.a. V_dot_target_initial) as high as stability allows. These changes are made in controller.h.
This switched Lyapunov controller does not handle mixed units very well. For example, if seven joints of a manipulator are being controlled, with six joints measured in radians and one measured in degrees, the degree measurement will be weighted more heavily and corrected more quickly than the other joints. For that reason, we recommend against mixing units. If your situation requires mixed units, then simply use two (or more) separate controllers.
For example, forces and torques are often mixed in a 6-vector. We recommend one controller for the 3x1 forces and another controller for the 3x1 torques (assuming they aren't coupled). If they are coupled, don't worry-- the controller will most likely still perform quite well.







